PROGRAMA PARA CALCULAR EL NÚMERO PI CON UNA PRECISIÓN

DE 14 DECIMALES

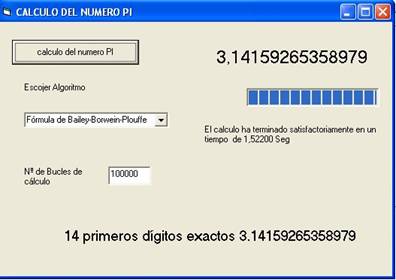
está basado en tres algoritmos para calcular el numero PI:

1- la fórmula de Leibnitz (1674):

π = 4 · ∑_i=0^∞ (-1)ⁱ / (2 · i + 1) Serie extremadamente lenta

la serie entre paréntesis tiene como límite pi / 4, por eso multiplicamos la serie global por 4, ojo que hemos hecho un bucle de 1000000000 ciclos y con un AMD 1900+ ha tardado 579 segundos (casi 10 minutos).

2- la fórmula de Wallis (1665):

π = 2 · Π_i=1^∞ 4 · i² / (4 · i² - 1)

3- la fórmula de Bailey-Borwein-Plouffe (2002):

π = ∑_i=0^∞ (1 / 16) ⁱ / (4 / ( 8 · i + 1) - 2 / ( 8 · i + 4) - 1 / ( 8 · i + 5) - 1 / ( 8 · i + 6))

El código de este programa es:

Dim pi As Double

Dim contador As Double

Dim i As Double

Dim TIEMPO1 As Double

Dim TIEMPO2 As Double

Dim maximo As Double

Dim formula As Integer

Private Sub Combo1_Click()

formula = Combo1.ListIndex

End Sub

Private Sub Command1_Click()

pi = 0

TIEMPO1 = Timer

Label1.Caption = ""

Label2.Caption = ""

Label1.Caption = "Calculando..."

Label2.Caption = "Comienza el calculo con precision de " & Text1.Text & " digitos"

maximo = CStr(Text1.Text)

pi = funcionformula(formula)

TIEMPO2 = Timer

Label1.Caption = Format(pi, "0.00000000000000")

Label2.Caption = "El calculo ha terminado satisfactoriamente en un tiempo de " & Format(TIEMPO2 - TIEMPO1, "0.####0") & " Seg"

cortar = False

maximo = 1

pi = 0

End Sub

Public Function funcionformula(opcion As Integer) As Double

Select Case opcion

Case 0:

' formula de Leibnitz

pi = 1: For i = 1 To maximo: ProgressBar1.Value = i * 100 / maximo: pi = pi + (-1) ^ i * (1 / (2 * i + 1)): Next i: pi = 4 * pi

' formula de Bailey-Borwein-Plouffe

Case 1:

pi = 1: For i = 1 To maximo: ProgressBar1.Value = i * 100 / maximo: pi = pi * 4 * i ^ 2 / (4 * i ^ 2 - 1): Next i: pi = pi * 2

' formula de Bailey-Borwein-Plouffe

Case 2:

For i = 0 To maximo: ProgressBar1.Value = i * 100 / maximo: pi = pi + (1 / 16) ^ i * (4 / (8 * i + 1) - 2 / (8 * i + 4) - 1 / (8 * i + 5) - 1 / (8 * i + 6)): Next i:

End Select

funcionformula = pi

End Function

Private Sub Form_Load()

pi = 0

i = 0

TIEMPO1 = 0

TIEMPO2 = 0

cortar = False

maximo = 10

Combo1.AddItem ("Fórmula de Leibnitz")

Combo1.AddItem ("Fórmula de Wallis")

Combo1.AddItem ("Fórmula de Bailey-Borwein-Plouffe")

Combo1.ListIndex = 0

formula = Combo1.ListIndex

End Sub